Numeracy
Numeracy
Numeracy, executing mathematics procedures fluently, precisely, and consistently with understanding is like reading fluently with comprehension. Reading comprehension is essential to access information from text. Numeracy and literacy are similar. Both processes engage us in seeking and making meaning. Mouthing words without comprehension is of little value. Similarly, recalling facts and executing a mathematics procedure, even fluently, without understanding the purpose and meaning of the procedure is of little value because it does not take us far in mathematics.
When reading, we need to know the contextual meaning of words and the objective of reading a passage. Similarly, in the context of mathematics, it is important that we know the answers to questions such as: Is the right procedure used here? What does this step in this procedure accomplish and why? Where does this step come from and what is its role in the procedure? Why does this procedure work in this problem? What do I expect as the answer? Am I right? Is this the most efficient way of doing this problem? Can I apply this method in different situations? Under what conditions does this procedure not work? Etc. The ability to answer these questions shows an understanding of mathematics concepts.
Answers to these questions and knowing the reasons behind procedures and the language and concepts associated with the procedures are essential for being a numerate person. Mastery of numeracy skills—fluency in the execution of the four arithmetic operations on whole numbers with precision, consistency and with understanding is like being able to read fluently with comprehension, being literate.
The statement learning to read by the third grade and then reading to learn defines the standards of competence in reading. Reading here means reading accurately, fluently, and with comprehension. To me, it has its counter part in mathematics: mastery of numeracy by the fourth grade and then using numeracy to learn mathematics. Numeracy means acquiring efficient and accurate strategies that lead to successful solutions of problems. Numeracy makes meaning of numbers and their relationships. Being numerate means (a) having the necessary mathematics concepts and skills to meet common quantitative and spatial demands, (b) having the confidence and intuition to apply quantitative principles in everyday life, and (c) being able to use these skills appropriately in diverse settings. In sum, being numerate requires the knowledge and disposition to think and act mathematically.
Numeracy: Learning Difficulties
Numeracy is the ability to execute standard whole number operations or algorithms correctly, consistently, and fluently and estimate, accurately and efficiently, both mentally and on paper, using a range of calculation strategies and means.
Acquisition of numeracy depends on proficiency in numbersense – the flexible use of number relationships and numerical information in various contexts. Those with numbersense can represent and use a number in multiple ways depending on the context and purpose. In computations and operations, they can decompose and recompose numbers with ease and fluency.
Numeracy is the gateway to higher mathematics beginning with the study of algebra and geometry. But, many individuals never reach this gateway because of difficulties with mastering numeracy. Some difficulties are caused by environmental factors:
lack of appropriate number experiences,
ineffective instruction and a fragmented curriculum,
inefficient conceptual models and strategies,
lack of appropriate skill development, and
low expectations.
For example, teaching arithmetic facts by sequential counting (“counting up” for addition, “counting down” for subtraction, “skip counting” on number line for multiplication and division), though advocated by many researchers and educators, is not an efficient strategy because one-to-one counting only turns most children into counters – that’s all.
Other difficulties in mastering numeracy are due to individual capacities and learning disabilities. Among those who exhibit learning problems in mathematics, some struggle in certain aspects of mathematics (e.g., procedures, conceptual processes). Some have difficulty in arithmetic, algebra, or geometry. Others display symptoms of dyscalculia, which manifests as poor number concept – difficulty in estimating the size and magnitude of numbers, lack of understanding and fluency in number relationships, and inefficiency of numerical operations.
A learning disability may manifest as deficits in the development of prerequisite skills: following sequential directions, spatial orientation/space organization, pattern recognition and extension, visualization and visual perception, and deductive and inductive thinking. These deficits may affect learning in different aspects of mathematics, for example, a few isolated skills in one concept or procedure or several areas of arithmetic and mathematics. Some learning problems fall in the intersection of quantity, language, and spatial thinking.
Because of the range of mathematics disabilities, we cannot always identify a cause or effect, and no one explanation adequately addresses the nature of learning problems in mathematics.


10 Digits Make all Numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
like 26 letters make all words.
Each digit represents an amount. Digits are less than 10.
Zero 0 represents nothing.


Addition, Plus, + Combine
0 = nothing
1 = 0 + 1
1 = 1 + 0
2 = 0 + 2
2 = 1 + 1
2 = 2 + 0
3 = 0 + 3
3 = 1 + 1 + 1
3 = 1 + 2
3 = 2 + 1
3 = 3 + 0
4 = 0 + 4
4 = 1 + 1 + 1 + 1
4 = 1 + 3
4 = 2 + 2
4 = 3 + 1
4 = 4 + 0
5 = 0 + 5
5 = 1 + 1 + 1 + 1 + 1
5 = 1 + 4
5 = 2 + 3
5 = 3 + 2
5 = 4 + 1
5 = 5 + 0
6 = 0 + 6
6 = 1 + 1 + 1 +
1 + 1 + 1
6 = 1 + 5
6 = 2 + 4
6 = 3 + 3
6 = 4 + 2
6 = 5 + 1
6 = 6 + 0
7 = 0 + 7
7 = 1 + 1 + 1
+ 1 + 1 + 1 + 1
7 = 1 + 6
7 = 2 + 5
7 = 3 + 4
7 = 4 + 3
7 = 5 + 2
7 = 6 + 1
7 = 7 + 0
8 = 0 + 8
8 = 1 + 1 + 1 + 1 +
1 + 1 + 1 + 1 +
8 = 1 + 7
8 = 2 + 6
8 = 3 + 5
8 = 4 + 4
8 = 5 + 3
8 = 6 + 2
8 = 7 + 1
8 = 8 + 0
9 = 0 + 9
9 = 1 + 1 + 1
1 + 1 + 1
1 + 1 + 1
9 = 1 + 8
9 = 2 + 7
9 = 3 + 6
9 = 4 + 5
9 = 5 + 4
9 = 6 + 3
9 = 7 + 2
9 = 8 + 1
9 = 9 + 0
MAKING TEN
10 = 0 + 10
10 = 1 + 9
10 = 2 + 8
10 = 3 + 7
10 = 4 + 6
10 = 5 + 5
10 = 6 + 4
10 = 7 + 3
10 = 8 + 2
10 = 9 + 1
10 = 10 + 0
TEENS NUMBERS
TEN + A DIGIT
10 = 10 + 0
11 = 10 + 1
12 = 10 + 2
13 = 10 + 3
14 = 10 + 4
15 = 10 + 5
16 = 10 + 6
17 = 10 + 7
18 = 10 + 8
19 = 10 + 9
Ten 10
Eleven
one + ten = 11
Twelve
two + ten = 12
Thirteen
three + ten = 13


Subtraction, Take Away, Remove
0 = nothing
1 - 0 = 1
1 - 1 = 0
2 - 0 = 2
2 - 1 = 1
2 - 2 = 0
3 - 0 = 3
3 - 1 - 1 - 1 = 0
3 - 1 = 2
3 - 2 = 1
3 - 3 = 0
4 - 0 = 4
4 - 1 - 1 - 1 - 1 = 0
4 - 1 = 3
4 - 2 = 2
4 - 3 = 1
4 - 4 = 0
5 - 0 = 5
5 - 1 - 1 - 1- 1-1 = 0
5 - 1 = 4
5 - 2 = 3
5 - 3 = 2
5 - 4 = 1
5 - 5 = 0
6 - 0 = 6
6 - 1 - 1 - 1 -
1 - 1 - 1 = 0
6 - 1 = 5
6 - 2 = 4
6 - 3 = 3
6 - 4 = 2
6 - 5 = 1
6 - 6 = 0
7 - 0 = 7
7 - 1 - 1 - 1
- 1 - 1 - 1 - 1 = 0
7 - 1 = 6
7 - 2 = 5
7 - 3 = 4
7 - 4 = 3
7 - 5 = 2
7 - 6 = 1
7 - 7 = 0
8 - 0 + 8
8 - 1 - 1 - 1 - 1 -
1 - 1 - 1 - 1 = 0
8 - 1 = 7
8 - 2 = 6
8 - 3 = 5
8 - 4 = 4
8 - 5 = 3
8 - 6 = 2
8 - 7 = 1
8 - 8 = 0
9 - 0 = 9
9 - 1 - 1 - 1
1 - 1 - 1
1 - 1 - 1 = 0
9 - 1 = 8
9 - 2 = 7
9 - 3 = 6
9 - 4 = 5
9 - 5 = 4
9 - 6 = 3
9 - 7 = 2
9 - 8 = 1
9 - 9 = 0
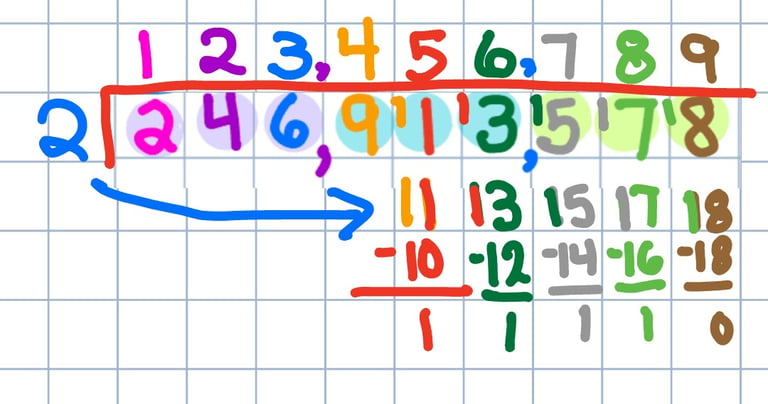
MAKING TEN
10 - 0 = 10
10 - 1 = 9
10 - 2 = 8
10 - 3 = 7
10 - 4 = 6
10 - 5 = 5
10 - 6 = 4
10 - 7 = 3
10 - 8 = 2
10 - 9 = 1
10 - 10 = 0
10 - 0 = 10
11 - 1 = 10
12 - 2 = 10
13 - 3 = 10
14 - 4 = 10
15 - 5 = 10
16 - 6 = 10
17 - 7 = 10
18 - 8 = 10
19 - 9 = 10
20 - 10 = 10
9 + 1 = 10
9 + 2 = 10 + 2 - 1
9 + 3 = 10 + 3 - 1
9 + 4 = 10 + 4 - 1
9 + 5 = 10 + 5 - 1
9 + 6 = 10 + 6 - 1
9 + 7 = 10 + 7 - 1
9 + 8 = 10 + 8 - 1
9 + 9 = 10 + 9 - 1
9 + 10 = 19
9 + 11 = 10 + 9 + 1 = 20
Double Numbers
0 + 0 = 0
1 + 1 = 2
2 + 2 = 4
3 + 3 = 6
4 + 4 = 8
5 + 5 = 10
6 + 6 = 12
7 + 7 = 14
8 + 8 = 16
9 + 9 = 18
10 + 10 = 20
11 + 11 = 22
12 + 12 = 24
Multiplication (Adding the same thing multiple times) & Division (Subtracting the same thing multiple times).
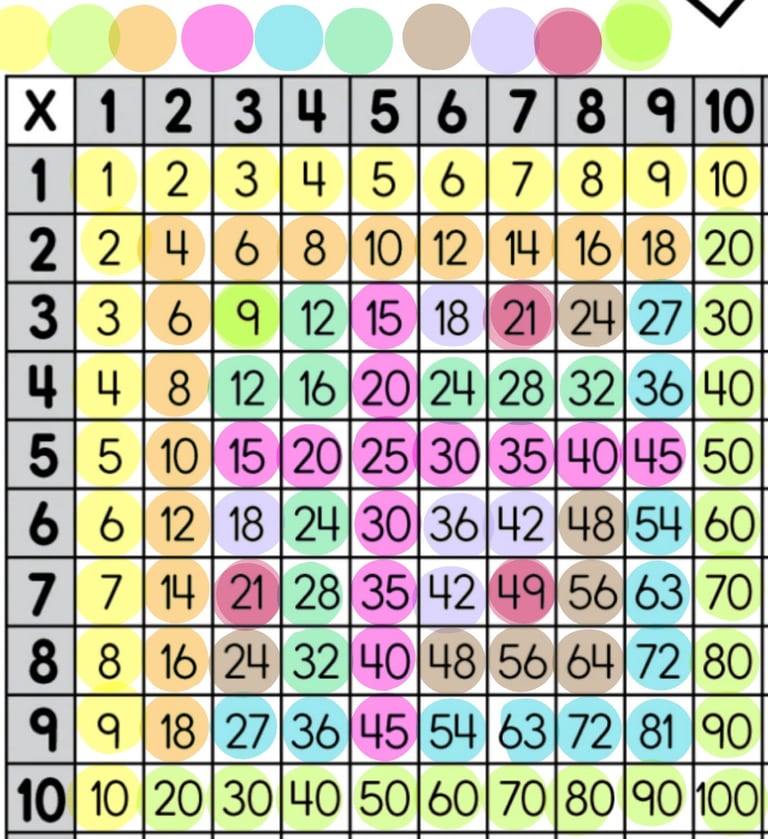
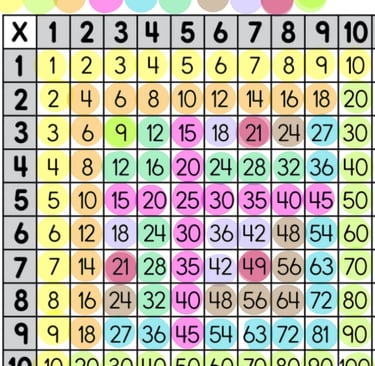
Practice facts many ways:
Add - Subtract:
4 + 5 = 9
4x + 5x = 9x
4xy + 5xy = 9xy
4xyz + 5xyz = 9xyz
40 + 50 = 90
400 + 500 = 900
4,000 + 5,000 = 9,000
4/10 + 5/10 = 9/10
.4 + .5 = .9
4 million + 5 million = 9 M
9 - 5 = 4
.9 - .4 = .5
9/10 - 5/10 = 4/10
9M - 4M = 5M
9¢ - 5¢ = 4¢
$9 - $4 = $5
9/1000 - 5/1000 = 4/1000
9/k - 4/k = 5/k
-5 - 4 = -5
Multiply - Divide:
7 × 9 = 63
9 × 7 = 63
.9 × .7 = .63
63 ÷ 7 = 9
63 ÷ 9 = 7
63x ÷ 7x = 9x
63x ÷ 9x = 7x
63/7 = 9
63/9 = 7
63/10 ÷ 9/10 = 7/10
63/10 ÷ 7/10 = 9/10
63,000 ÷ 9,000 = 7,000
63,000 ÷ 7,000 = 9,000
630 ÷ 90 = 70
630 ÷ 70 = 90
6,300 ÷ 900 = 700
6,300 ÷ 700 = 900
63M ÷ 9M = 7M
63GB ÷ 9GB = 7GB
Multiply - Divide Practice
Example:
3 + 3 + 3 + 3 = 12
3 × 4 = 12
4 × 3 = 12
3(4)= 12
4(3)= 12
3*4 = 12
4*3 = 12
4 • 3 = 12
3 • 4 = 12
Example:
3a + 3a + 3a + 3a = 12a
3a × 4 = 12a
4a × 3 = 12a
3(4a)= 12a
4a(3)= 12a
3a*4 = 12a
4*3a = 12a
4a • 3 = 12a
3a • 4 = 12a
Example:
3/10 + 3/10 + 3/10 + 3/10 = 12/10
3/10 × 4 = 12/10
4/10 × 3 = 12/10
3/10(4)= 12/10
4/10(3)= 12/10
3/10*4 = 12/10
4*3/10 = 12/20
.4 • .3 = .12
.3 • .4 = .12
Multiplication: Short vs. Long
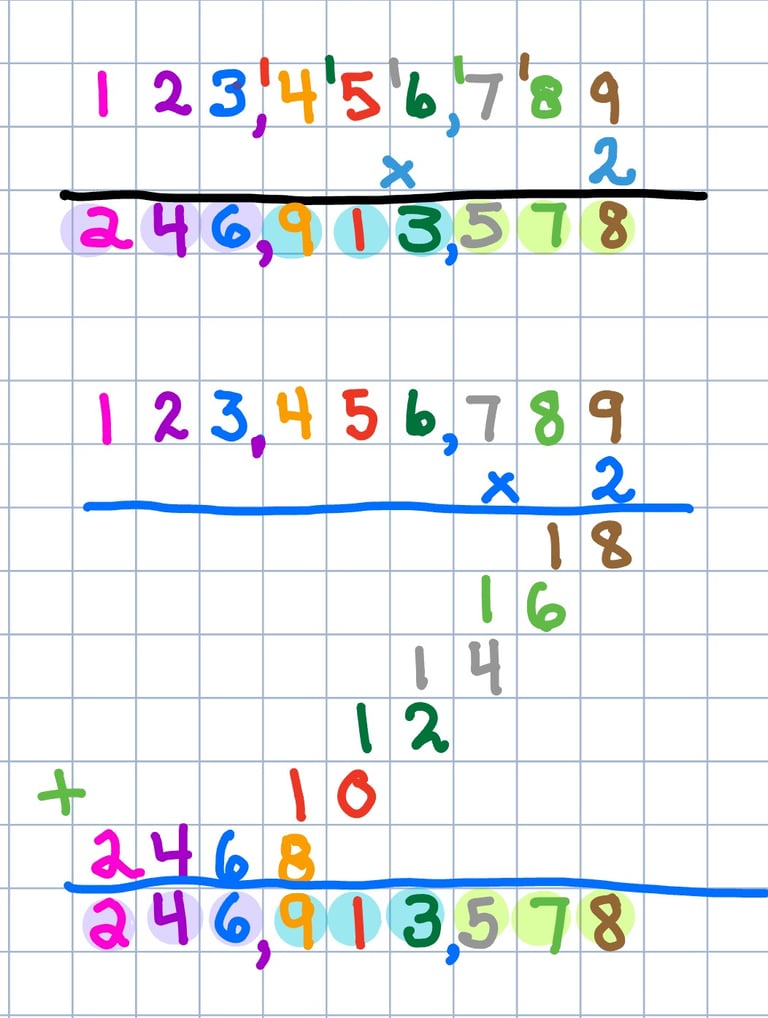
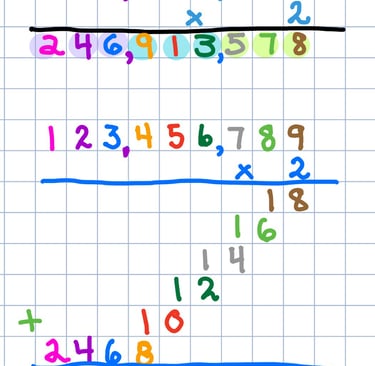
Multiply two digits from R to L, and add the leftovers, then write the product below the line in the column of the multiplicand.
Multiply two digits from R to L and write the product so it ends in the parking spot of the multiplicand. Sum each column.
Long Division

Divide the dividend by the divisor, from L to R. Write the quotient on top in the same column as the digit in the dividend.
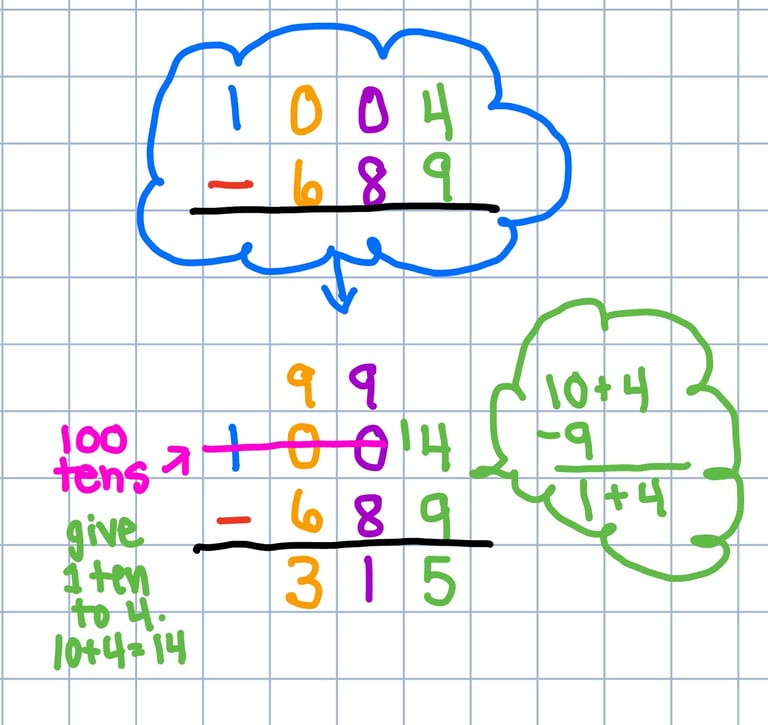
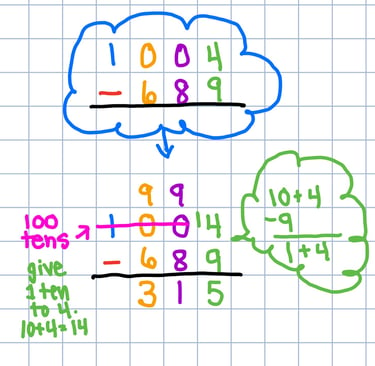
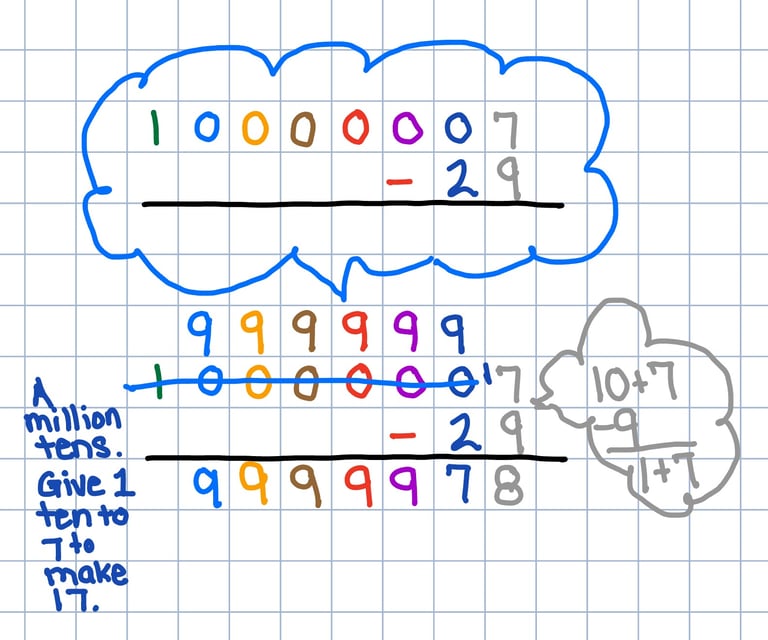
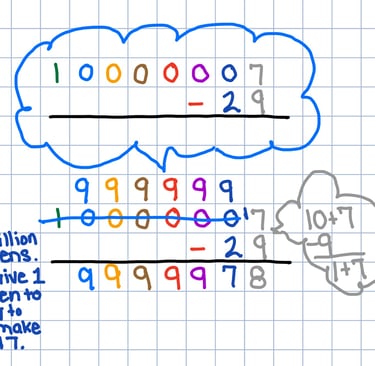
Minus - Give Ten, Make 10